LotkaVolterra

The Lotka-Volterra equations to model predator-prey-dynamics

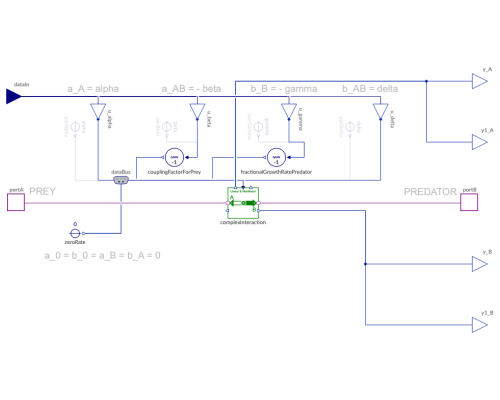
Diagram

Information

This information is part of the Business Simulation Library (BSL). Please support this work and ► donate.

These are the classical Lotka-Volterra equations describing predator-prey-dynamics in an idealized way [17]. The dynamics for the prey population (portA) and the predator population (portB) are given by the following equations:

Note: Capital letters were chosen to represent the stocks (state variables) connected at portA and portB in the formula above. Also dot notation is used for a stock's rate of flow—its first derivative with respect to time.

Coefficient	Unit	Description
`alpha`	1 per second	fractional growth rate for prey population
`beta`	1 per second per base unit of B (`TypeB`)	fractional rate of decline for prey population per predator
`gamma`	1 per second	fractional rate of decline for predator population
`delta`	1 per second per base unit of A (`TypeB`)	fractional rate of groth for predator population per prey

Notes

Within the components LinearInteraction and NonlinearInteraction the rates passed for a_B, a_AB, b_A, b_AB call for divison by a reference level of the connected stocks. In many cases, modelers can leave the type selectors TypeA, TypeB at their default value of Unspecified so that no conversion will take place.

Should unit conversion be needed, modeleres may wish to select appropriate type values and corresponding displayUnit settings to enter convenient reference levels refA, refB.

Parameters (10)

refA	Value: 1 Type: TypeA Description: Reference value, i.e., divisor, for the couplings b_A, b_AB
refB	Value: 1 Type: TypeB Description: Refrence value, i.e., divisor, for the couplings a_B, a_AB
alpha	Value: unspecified Type: Rate (1/s) Description: Fractional growth rate of prey population (A)
beta	Value: unspecified Type: Rate (1/s) Description: Fractional rate of decline for prey population (A) per predator
gamma	Value: unspecified Type: Rate (1/s) Description: Fractional rate of decline for predator population (B)
delta	Value: unspecified Type: Rate (1/s) Description: Fractional rate of growth for predator population (B) per prey
hasConstantAlpha	Value: false Type: Boolean Description: = true, if the constant parameter value is to be used instead of the input connector
hasConstantBeta	Value: false Type: Boolean Description: = true, if the constant parameter value is to be used instead of the input connector
hasConstantGamma	Value: false Type: Boolean Description: = true, if the constant parameter value is to be used instead of the input connector
hasConstantDelta	Value: false Type: Boolean Description: = true, if the constant parameter value is to be used instead of the input connector

Connectors (12)

	portA	Type: FlowPort Description: Flow from/to Stock A
	portB	Type: FlowPort Description: Flow to/from Stock B
	y_B	Type: RealOutput_B Description: Rate for flow to and from B (positive value indicates inflow)
	y1_B	Type: RealOutput_B Description: Rate for flow to and from B (positive value indicates inflow)
	y1_A	Type: RealOutput_A Description: Rate for flow to and from A (positive value indicates inflow)
	y_A	Type: RealOutput_A Description: Rate for flow to and from A (positive value indicates inflow)
	dataIn	Type: InputConnector Description: Inputs for predator-prey model
	u_alpha	Type: RealOutput Description: Output signal
	u_beta	Type: RealOutput Description: Output signal
	u_gamma	Type: RealOutput Description: Output signal
	u_delta	Type: RealOutput Description: Output signal
	dataBus	Type: DataBus Description: Expandable connector for multiple data signals (input/output)

Components (8)

	complexInteraction	Type: ComplexInteraction Description: Combined linear and nonlinear interaction
	zeroRate	Type: ConstantConverter Description: Zero rate input
	fractionalGrowthRatePredator	Type: Gain Description: Convert rate of delince to growth rate
	couplingFactorForPrey	Type: Gain Description: Convert rate of delince to growth rate
	parAlpha	Type: ConstantConverter Description: Constant alpha (optional)
	parBeta	Type: ConstantConverter Description: Constant beta (optional)
	parGamma	Type: ConstantConverter Description: Constant gamma (optional)
	parDelta	Type: ConstantConverter Description: Constant delta (optional)